If 6 - 5i is a root then 6 + 5i is also a root.

if the irrational number

a + 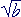is a root then

a -

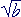
is also a root.

Suppose we know that 2 + is a root. What a is polynomial with this root?

Since we know
2 - is also a root we know, through our Factor Theorem that

(x - (2 - )) (x - (2 + )) = 0

So :

x² - 2x + x - 2x + 4 - x - x - 2 - 3 = 0

Which equals : x² - 4x + 4

---

Another way to look at this is to start with the equation.

Take x³ + 5x² + 11x + 15

If you guss one root is 3 and try it with synthetic division, you find out it factors to

(x -3)(x² + 2x + 5)

When we use the quadratic formula to factor x² + 2x + 5

we find the roots are -1 + sqrt(-4) or -1 - sqrt(-4)
which is -1 + 2i or -1 - 2i

These two roots are imaginary. They don't hit the x line.

So, one of our roots is real and the other two are imaginary. Note : if we have 1 imaginary root then by definition we have two, because in the quadratic formula we have -b +- sqrt(discriminant). If the discriminant is negative then we have two imaginary roots.